What are graph embeddings ?

In the modern world of big data, graphs are undoubtedly essential data representation and visualization tools.

Imagine navigating a city without a map. When working with complicated networks, such as social relationships, molecular structures, or recommendation systems, data analysts frequently encounter similar difficulties. Here's where graph embeddings come into play. They allow researchers and data analysts to map nodes, edges, or complete graphs to continuous vector spaces for in-depth data analysis.

What are graph embeddings and how do they work? In this guide, we examine the fundamentals of graph embeddings, including:

• What are graph embeddings
• How graph embeddings work
• Benefits of graph embeddings
• Trends in graph embeddings

This guide will help you uncover the mysteries contained in graphs, whether you are a data analyst, researcher, or someone just interested in learning more about the potential of network analysis. Continue reading!

Fundamentals of graphs

A graph is a slightly abstract representation of objects that are related to each other in some way, and of these relationships. Typically, the objects in a graph database are drawn as dots called vertices or nodes. A line (or curve) connects any two vertices representing objects that are related or adjacent; such a line is called an edge.

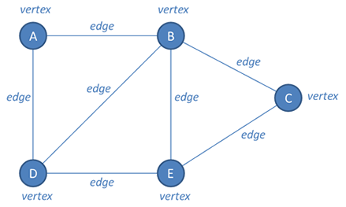
It is a simplified map where lines represent relationships and dots represent items. These dots, or vertices, hold information about the entities, while the lines, or edges, represent the connections between the entities.

After learning about the vertices and edges that comprise a graph, let's investigate some of its unrealized possibilities: graph embeddings.

What are graph embeddings?

Graph embedding refers to the process of representing graph nodes as vectors which encode key information of the graph such as semantic and structural details, allowing machine learning algorithms and models to operate on them. In other words they are basically low-dimensional, compact graph representations that store relational and structural data in a vector space. Graph embeddings, as opposed to conventional graph representations, condense complicated graph structures into dense vectors while maintaining crucial graph features, potentially saving time and money in processing.

Ever wondered how your social media knows to suggest perfect friends you never knew existed? Or how your phone predicts the traffic jam before you even hit the road? The answer lies in a hidden world called graphs, networks of connections, like threads linking people, places, and things. And to understand these webs, we need a translator: graph embeddings.

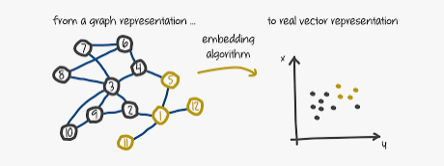
Think of them as a magic trick that transforms intricate networks of vertices and edges into compact numerical representations. These "embeddings" capture the essence of each node (vertex) and its relationship to others, distilling the complex network into a format readily understood by machine learning algorithms.

Benefits of graph embeddings

Being able to represent data using graph embedding offers great benefits, including:

1. Graph embeddings allow researchers and data scientists to explore hidden patterns within large networks of data. This greatly enhances the accuracy and efficiency of machine learning algorithms
2. By identifying hidden patterns, researchers can make informed decisions and come up with better solutions for complex problems.
3. Graph embedding distills complex graph-structured data and represents them as simple numerical figures, making computation operations on them very easy and fast. This benefit allows even the most complex algorithms to be scaled to fit all sorts of datasets.

Techniques for generating graph embeddings

Graph embedding algorithms and node embedding techniques are the two main kinds of techniques used to construct graph embeddings.

1. Node embedding techniques

These techniques focus on representing individual nodes within the graph as unique vectors in a low-dimensional space. Imagine each node as a distinct character in a complex story, and these techniques aim to capture their essence and relationships through numerical encoding.

i). DeepWalk

Inspired by language modeling, DeepWalk treats random walks on the graph as sentences and learns node representations based on their "context" within these walks. Think of it as understanding a word better by its surrounding words in a sentence.

ii). Node2Vec

Building on DeepWalk, Node2Vec allows for flexible exploration of the graph by controlling the balance between breadth-first and depth-first searches. This "adjustable lens" allows for capturing both local and global structural information for each node.

iii). GraphSAGE

This technique focuses on aggregating information from a node's local neighborhood to create its embedding. Imagine summarizing a person based on their close friends and associates. GraphSAGE efficiently handles large graphs by sampling fixed-size neighborhoods for each node during training.

2. Graph embedding algorithms

While node embedding techniques concentrate on specific nodes, graph algorithms try to capture the interactions and general structure of the entire network. Think of them as offering a thorough summary of the network that accounts for each node individually as well as its connections.

i). Graph Convolutional Networks (GCNs)

GCNs function directly on the graph structure, executing convolutions on adjacent nodes to represent their interconnection. They were inspired by convolutional neural networks for images. Consider applying a filter to an image that takes into account not only a pixel but also the pixels surrounding it.

ii). Graph Attention Networks (GATs)

Expanding upon GCNs, GATs incorporate an attention mechanism that enables the network to concentrate on the most pertinent neighbors for every node, perhaps resulting in more precise depictions.

iii). Graph Neural Networks (GNNs)

Refers to a variety of graph data processing and node representation learning frameworks. Their approach blends concepts from conventional neural networks with graph-specific processes to extract structure information as well as node attributes.

Keep in mind that the subject of graph embedding is continually changing, with new methods and improvements appearing on a regular basis.

Applications of graph embeddings

Due to their ability to turn graph data into a computationally processable format, graph embedding is useful in graph pre-processing. Before we get to the use cases, let's look at the capabilities that provide the foundation that inform the use cases for graph embeddings:

Graph Analytics	Graph embeddings make it easy to gain insight into the structure, patterns and relationships in graphs
Machine Learning and Deep Learning	Graph embeddings make it possible to represent graph data as continuous data, making it useful in natural language processing and training of various models such as recurrent neural networks
Measuring the similarity between two vectors	Graph embedding makes it easy to understand how users interact with items

Based on the above capabilities, graph embeddings find wide-ranging applications in several disciplines due to their capacity to capture intricate interactions inside graphs and represent them in low-dimensional vector spaces.

Here are some important use cases.

1. Social Network Analysis

In social network analysis, graph embeddings facilitate community detection, user behavior prediction, and identification of influential nodes.

Consider Facebook as an example, where graph embeddings help uncover communities of users, predict friendship connections, and identify influential users based on their interactions and network centrality.

2. Recommendation Systems

Graph embeddings power recommendation systems by modeling user-item interactions and capturing recommendation graph structures.

For example, systems like Netflix and YouTube use graph embeddings to recommend movies and videos based on users' past movie ratings among other metrics

3. Knowledge Graphs

In knowledge graphs, graph embeddings enable query response, entity linking, and semantic similarity computation.

The accessibility and interpretability of knowledge graphs are improved by integrating entities and relations.

4. Biological Networks and Bioinformatics

Graph embeddings are used in the analysis of biological networks, including gene regulatory networks and protein-protein interactions.

They can be used to detect gene-disease connections, accelerate drug discovery, and predict targets and protein functions by foreseeing target-drug interactions.

5. Fraud Detection and Anomaly Detection

It is critical to safeguard users and financial systems against fraud. Graph embeddings play a critical role in fraud and anomaly detection systems by enabling the identification of anomalous patterns in networks such as social networks and financial transactions.

Also Read: Fraud Detection With Graph Analytics

Metrics for evaluating graph embeddings

It's not enough to only create strong graph embeddings; we also need instruments to evaluate them.

Metrics for Evaluating Graph Embeddings measure how well graph embedding methods capture and maintain the relational and structural information in graphs.

Important measurements include:

• Node Classification Accuracy: Indicates how well nodes' properties and relationships can be captured by using learned embeddings to predict their labels.
• Link Prediction Accuracy measures how well a graph's learned embeddings may be used to predict future or missing edges, demonstrating how well graph topology is captured.
• Graph Reconstruction: Measures the degree to which graph attributes can be preserved by reconstructing the original graph structure using learned embeddings.
• Downstream Task Performance: Measuring downstream task performance with learned embeddings shows how useful downstream machine learning tasks are in practical applications.
• Embedding Quality: Assesses the degree of similarity preservation, dimensionality reduction, and computing efficiency that make up learned embeddings.

All things considered, these measures offer thorough insights into the effectiveness and generalizability of graph embedding methods across a range of fields and applications.

Challenges in generating effective graph embeddings and how to overcome them

It can be difficult to generate efficient graph embeddings since analysts have to reduce the dimensionality of the graph while maintaining its structural information.

As a result, creating graph embeddings often encounters these primary issues:

Scalability issues

Accurate and efficient embeddings of graphs can be challenging to produce due to their huge size and complexity. Scalability is an important concern, especially in the processing of real-world applications where the graphs might be of huge size and keep on changing.

Heterogeneity issues

You can encounter challenges in representing the structural information of a network in a low-dimensional space because nodes and edges in graphs have varying types and properties.

Sparsity issues

A large number of nodes and edges in some networks may lack connections, making them extremely sparse. Because of this, it could be challenging to represent the graph's structural information in a low-dimensional space.

To overcome these challenges, researchers have developed several techniques and algorithms for generating effective graph embeddings including sampling strategies, skip connections, inductive learning, and adversarial training.

Future trends in graph embeddings

The future of graph embeddings is shaped by these emerging trends, mostly aimed at addressing evolving complexities.

• Dynamic graphs require adaptive embedding techniques.
• Interpretability is vital, with many techniques seen as opaque "black boxes." Demand will continue to grow for interpretable methods providing transparent insights.
• Efficiency will remain crucial amid growing graph complexity. Techniques must balance accuracy with computational efficiency.
• Scalable algorithms tailored to dynamic and multi-modal graphs will rise. They prioritize interpretability, offering clear explanations.

In summary, the future of graph embeddings relies on adaptive, interpretable, and efficient techniques navigating dynamic, multi-modal graph data, fostering innovation across domains.

Conclusion

Graph embeddings have made it possible to untangle complex networks and reveal hidden connections. From social media analysis to drug discovery, their applications are vast.

While challenges like scalability and interpretability persist, the future shines bright with dynamic and multi-modal techniques.

NebulaGraph supports graph embeddings and is available in AWS and Azure. Get started with a Free Trial and witness the power of connections truly unveiled.